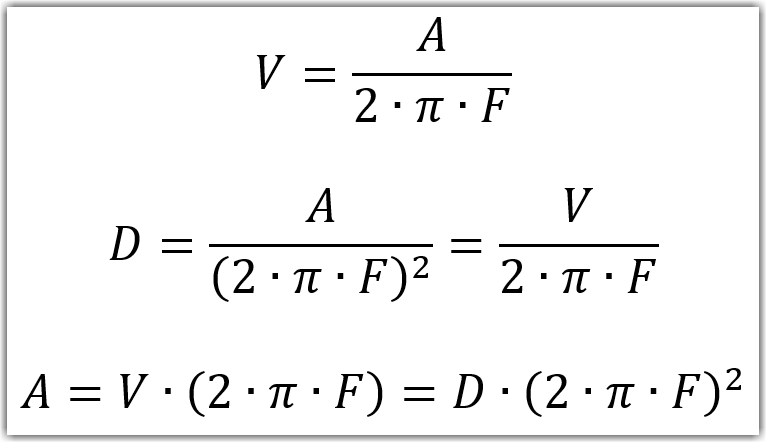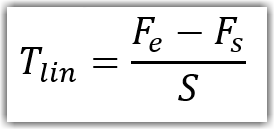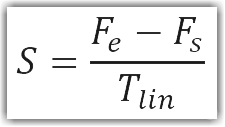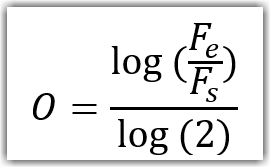lv
en
Products
Products
Solutions
Knowledge
Support
Downloads
News
Contact
Company
Data acquisition systems, recorders, spectrum analyzers RL-C21M
Vibration control systems RL-C21
Vibration control systems RL-C25
Data acquisition systems, recorders, spectrum analyzers RL-R19
Data acquisition systems, recorders, spectrum analyzers RL-R17
Amplifiers RL-A200
Amplifiers RL-A500
Amplifiers RL-A1000
Amplifiers RL-S039
Software TestUp
Software SignalUp
Software LogUp
Software Sensor Calibration
View All products

Sine

Relation between Acceleration, Velocity, and Displacement

The formulas here describe the relation between acceleration, velocity, and displacement. The formulas are:

The Most Common Formulas of Sine and Random — Relations between Acceleration, Velocity and Displacement

where:

  • A – acceleration in m/s2;
  • V – velocity in m/s;
  • D – displacement in m. Please note that displacement D is listed in a zero-to-peak value;
  • F – sine frequency in Hz.

We then use the above relations to derive the formulas for crossover points in Sine tests:

The Most Common Formulas of Sine and Random — for smoothing crossover point or sweep frequency sine test

where:

  • A – acceleration in m/s2
  • V – velocity in m/s;
  • D – displacement in m. Please, note that displacement D is listed in zero-to-peak value;
  • Dmm – displacement D in mm.
  • F(A-V) — crossover point between acceleration and velocity;
  • F(V-D) — crossover point between velocity and displacement;
  • F(A-D) — crossover point between acceleration and displacement.

Sweep rate calculations

There are two common sweep rate types in Sine: linear and logarithmic. The linear sweep rate is usually nominated in Hz/sec, the logarithmic — in oct/min.

We can calculate the sweep time of a linear sweep using the following formula:

The Most Common Formulas of Sine and Random — Sweep rate calculations

where: 

  • Tlin – sweep time in seconds;
  • Fe – end sweep frequency;
  • Fs – start sweep frequency;
  • S – sweep rate.

Vice versa, the required sweep rate can be calculated using the desired sweep time:

The Most Common Formulas of Sine and Random — Sweep rate calculations

If we are speaking of the logarithmic sweep rate, the base term here is an octave – the interval between a frequency and its double value.

Therefore, if we want to know the number of octaves between sweep frequencies, we have to use the formula below:

The Most Common Formulas of Sine and Random — octaves and sweep frequencies

Using the formula below, we can calculate the sweep time of a logarithmic sweep:

The Most Common Formulas of Sine and Random — sweep time of a logarithmic sweep

where Tlog is the logarithmic sweep time in seconds.

The required sweep rate also can be calculated using the following formula:

The Most Common Formulas of Sine and Random — sweep rate

Random vibration

Calculation of Acceleration RMS value

Generally, a random profile is defined as a table of PSD and frequency, as shown below:

Frequency (Hz) Amplitude, g2/Hz
20 0.00040
100 0.01
1000 0.01
2000 0.0025

The Most Common Formulas of Sine and Random — Random vibration - Spectrum density vs. Frequency

To calculate the RMS value of acceleration we should calculate the area under the task line. This requires two actions: 1) calculating the area under each line of the spectrum and 2) summing the areas.

The best way to calculate the area depends on the slope of the line. The slope can be calculated using the formula: 

where:

  • Ae – end amplitude;
  • As – start amplitude;
  • Sl – slope.

The area P is calculated using the formula:

The Most Common Formulas of Sine and Random — The area P - RMS value of the acceleration

The acceleration RMS value is calculated using:

The Most Common Formulas of Sine and Random — RMS value

Calculation of Velocity and Displacement Values

Calculating velocity is based on the same principle, as calculating the acceleration, however. the values of amplitude are divided by (2π)2:

The Most Common Formulas of Sine and Random — Calculation of Velocity and Displacement Values

Two peculiarities have to be mentioned here:

  • As and Ae should be in (m/s2)2/Hz units;
  • not RMS, but peak values are usually taken into account. Therefore, we have to multiply the RMS value by the sigma factor:

​The Most Common Formulas of Sine and Random — RMS value on sigma factor

where ς– sigma factor.

The same principle is used for displacement calculations:

The Most Common Formulas of Sine and Random — displacement calculations - RMS value

However, the third peculiarity appears here: Dpeak is a zero-to-peak value, so if we want to calculate the peak-to-peak value, we have to multiply Dpeak by two:

The Most Common Formulas of Sine and Random — Dpeak is a zero-peak value

If you want to learn more about the formulas we use, contact our 24/7 technical support via email or call +371 6610 2166.

Products
Solutions
Knowledge
Company
Contact us
+371 6610 2166
Support
Join Us
© 2024 RULA Technologies
Processing Policy

Polityka Prywatności

Welcome to our Privacy Policy


Your privacy is critically important to us.
RULA Technologies is located at:
Balta iela 7, Riga, LV-1055, Latvia


It is RULA Technologies's policy to respect your privacy regarding any information we may collect while operating our website. This Privacy Policy applies to https://rula-tech.com (hereinafter, "us", "we", or "https://rula-tech.com"). We respect your privacy and are committed to protecting personally identifiable information you may provide us through the Website. We have adopted this privacy policy ("Privacy Policy") to explain what information may be collected on our Website, how we use this information, and under what circumstances we may disclose the information to third parties. This Privacy Policy applies only to information we collect through the Website and does not apply to our collection of information from other sources.
Depending on your activities when visiting our Website, you may be required to agree to additional terms and conditions.


- Website Visitors


Like most website operators, RULA Technologies collects non-personally-identifying information of the sort that web browsers and servers typically make available, such as the browser type, language preference, referring site, and the date and time of each visitor request. RULA Technologies's purpose in collecting non-personally identifying information is to better understand how RULA Technologies's visitors use its website. From time to time, RULA Technologies may release non-personally-identifying information in the aggregate, e.g., by publishing a report on trends in the usage of its website.
RULA Technologies also collects potentially personally-identifying information like Internet Protocol (IP) addresses for logged in users and for users leaving comments on https://rula-tech.com. RULA Technologies only discloses logged in user and commenter IP addresses under the same circumstances that it uses and discloses personally-identifying information as described below.


- Gathering of Personally-Identifying Information


Certain visitors to RULA Technologies's websites choose to interact with RULA Technologies in ways that require RULA Technologies to gather personally-identifying information. The amount and type of information that RULA Technologies gathers depends on the nature of the interaction. For example, we ask visitors who sign up at https://rula-tech.com to provide a username and email address


- Security


The security of your Personal Information is important to us, but remember that no method of transmission over the Internet, or method of electronic storage is 100% secure. While we strive to use commercially acceptable means to protect your Personal Information, we cannot guarantee its absolute security.


- Links To External Sites


Our Service may contain links to external sites that are not operated by us. If you click on a third party link, you will be directed to that third party's site. We strongly advise you to review the Privacy Policy and terms and conditions of every site you visit.
We have no control over, and assume no responsibility for the content, privacy policies or practices of any third party sites, products or services.


- Protection of Certain Personally-Identifying Information


RULA Technologies discloses potentially personally-identifying and personally-identifying information only to those of its employees, contractors and affiliated organizations that (i) need to know that information in order to process it on RULA Technologies's behalf or to provide services available at RULA Technologies's website, and (ii) that have agreed not to disclose it to others. Some of those employees, contractors and affiliated organizations may be located outside of your home country; by using RULA Technologies's website, you consent to the transfer of such information to them. RULA Technologies will not rent or sell potentially personally-identifying and personally-identifying information to anyone. Other than to its employees, contractors and affiliated organizations, as described above, RULA Technologies discloses potentially personally-identifying and personally-identifying information only in response to a subpoena, court order or other governmental request, or when RULA Technologies believes in good faith that disclosure is reasonably necessary to protect the property or rights of RULA Technologies, third parties or the public at large.
If you are a registered user of https://rula-tech.com and have supplied your email address, RULA Technologies may occasionally send you an email to tell you about new features, solicit your feedback, or just keep you up to date with what's going on with RULA Technologies and our products. We primarily use our News page to communicate this type of information, so we expect to keep this type of email to a minimum. If you send us a request (for example via a support email or via one of our feedback mechanisms), we reserve the right to publish it in order to help us clarify or respond to your request or to help us support other users. RULA Technologies takes all measures reasonably necessary to protect against the unauthorized access, use, alteration or destruction of potentially personally-identifying and personally-identifying information.


- Aggregated Statistics


RULA Technologies may collect statistics about the behavior of visitors to its website. RULA Technologies may display this information publicly or provide it to others. However, RULA Technologies does not disclose your personally-identifying information.


- Cookies


To enrich and perfect your online experience, RULA Technologies uses "Cookies", similar technologies and services provided by others to display personalized content, appropriate advertising and store your preferences on your computer.
A cookie is a string of information that a website stores on a visitor's computer, and that the visitor's browser provides to the website each time the visitor returns. RULA Technologies uses cookies to help RULA Technologies identify and track visitors, their usage of https://rula-tech.com, and their website access preferences. RULA Technologies visitors who do not wish to have cookies placed on their computers should set their browsers to refuse cookies before using RULA Technologies's websites, with the drawback that certain features of RULA Technologies's websites may not function properly without the aid of cookies.
By continuing to navigate our website without changing your cookie settings, you hereby acknowledge and agree to RULA Technologies's use of cookies.
Privacy Policy Changes
Although most changes are likely to be minor, RULA Technologies may change its Privacy Policy from time to time, and in RULA Technologies's sole discretion. RULA Technologies encourages visitors to frequently check this page for any changes to its Privacy Policy. Your continued use of this site after any change in this Privacy Policy will constitute your acceptance of such change.


- Processing Policy  
- Credit & Contact Information


This privacy policy was created at https://termsandconditionstemplate.com/privacy-policy-generator/.
If you have any questions about this Privacy Policy, please contact us via email or phone.